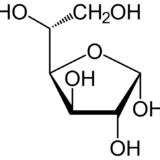
希薄溶液の溶質は気体分子の状態と似ているから
浸透圧はΠV=nRTで表すことができることが知られています。このRは気体定数と呼ばれ、気体の状態方程式で出現する数字です。浸透圧と気体にどのような関係があるのでしょうか。
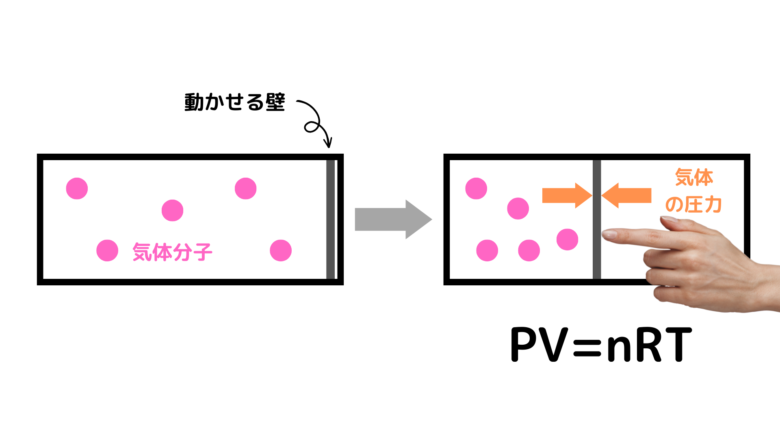
例えば、次のような動く壁がつけられた容器を準備します。この壁を押して移動した時、壁にかかる気体の圧力は気体の状態方程式(PV=nRT)で求めることができます。
一方、希薄溶液でも動く半透膜がつけられた容器を準備します(図では溶媒分子を省略して書いています)。この壁を移動した時、壁にかかる圧力は浸透圧です。
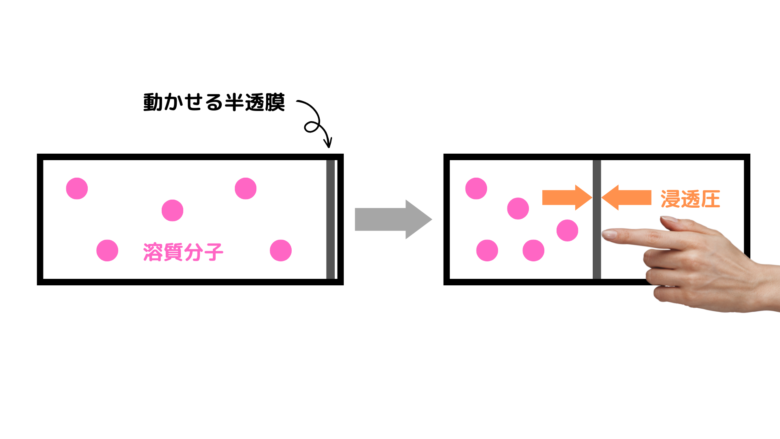
先ほどの気体の図と比較してみると、非常に似ていますね。ファントホッフはここに着目し、「溶液の浸透圧とは、溶液中からすべての溶媒分子を取り除いたと仮定したとき、溶質粒子の自由な運動によって引き起こされる圧力である」として、ΠV=nRTが成り立つことを説明しました。
他の説明の仕方
浸透圧は溶媒が移動することによって起こる圧力です。浸透圧は浸透が起こらないよう(体積が変化しないように)に押さえる圧力と等しいとも言えます。
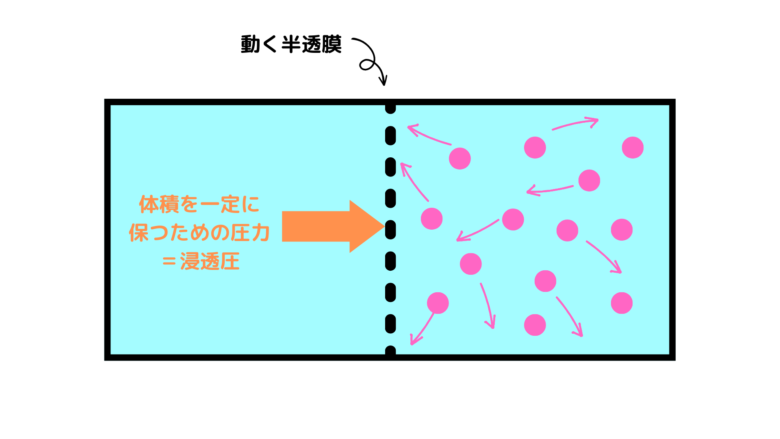
この圧力は、溶質が壁にぶつかって押す力と同じものとして解釈することができます(溶媒は壁をすり抜けるのでぶつからない)。そうすると、希薄溶液の溶質分子はもはや気体の粒子とあまり変わらない働きをするため、気体の状態方程式とやはり近くなるのです。
浸透圧は厳密に気体の状態方程式と一致するの?
そもそも気体の状態方程式は理想気体(分子の体積0、分子間力無し)でのみ成り立つ式でした。実在気体では、低圧、高温条件が求められます。希薄溶液では、低圧=濃度が薄い状態は作れますが、高温状態は気化してしまうため難しいでしょう(超頑丈な密閉した容器ならば可能ですが…)。その結果、分子間力の影響が大きくでることになり、たいした設備のない環境では気体の状態方程式と一致することは実際は難しいです。