状態方程式とは
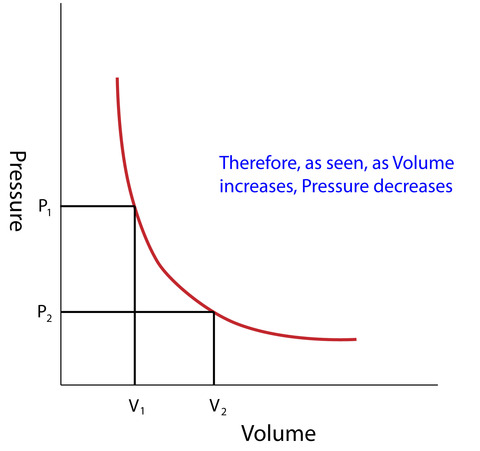
ボイルの法則により、体積（V）は圧力（P）に反比例する。また、シャルルの法則により、体積（V）は絶対温度（T）に比例する。これらは、物質量（n）が一定の時のみの法則である。ボイル・シャルルの法則によれば、PV / Tは一定になる。
ボイル・シャルルの法則と、アボガドロの「気体1molは、０℃、1atmにおいて22.4Lである」との法則を合わせて、PV / Tの値を求めると、
PV / T = 1atm × 22.4L / 273K = 0.082(atm･L/K･mol)
この0.082を気体定数（R）と呼ぶ。Rは8.3J/(K・mol)と変換することもできる。上記の式はあくまで1molの場合である。2molの場合では2Rに、3molの場合では3Rになる。つまり、次の式となる。
PV / T = nR
このTを左辺に移動したものが、気体の状態方程式である。
PV = nRT
http://function-ltd.com/PoS/?p=32
なぜ0.082 atm・L = 8.3 Jなのか
1Jとは1Nの力で物質を1m移動させる仕事に相当する。よって、1J = 1 Nm（ニュートン×メートル）である。またatmとLは次のように変換できる。
1 atm = 1.013 ×105 Pa
1 L = 0.001 m3 …②
Paは1m2あたりにかかる力Nであるから、単位はN/m2に変換できる。よって次のようになる。
1 atm = 1.013 ×105 Pa = 1.013 × 105 N/m2 …①
①と②を0.082 atm・Lに代入すると
0.082 × 1.013 × 105 ×0.001 (N/m2 × m3)
= 8.3 (Nm) = 8.3 J
よって、0.082 atm・L = 8.3 Jとなる。
気体の状態方程式と分子量の求め方
分子量をMとすると、気体w(グラム)の物質量n(mol)は、n(mol) = w(g) / M(g/mol)となる。また、気体の密度d(g/L)は、d = w (g)/ V(L)である。
よってPV = nRTに代入すると、次の式が立てられる。
PV = w/M ×RT、変形するとM=wRT/PV
d=w/Vなので次のようにも変形できる。
M = dRT/P
Which came first, the problem or the sotnoilu? Luckily it doesn’t matter.
Ya learn somhietng new everyday. It’s true I guess!