ボイルは、温度が一定の時、気体の体積は圧力に反比例するという法則を発見しました。反比例すると、次の表のようになります(数値は例です)。
| 体積 V | 22.4L | 11.2L | 5.6L | 2.8L |
| 圧力 P | 1気圧 | 2気圧 | 3気圧 | 4気圧 |
よって次の式が建てられます。
P1V1 = P2V2(Pは圧力、Vは体積)
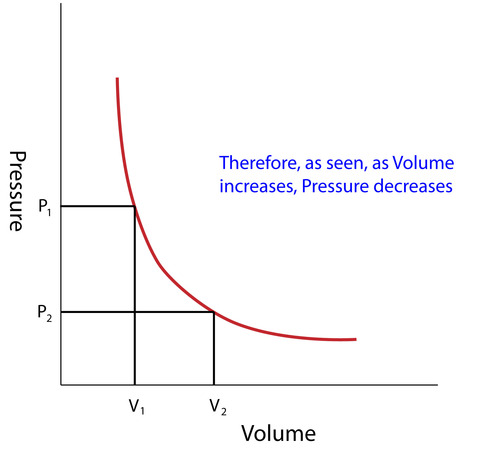

つまり、体積を小さくすれば圧力は高くなるし、体積を大きくすれば圧力は小さくなるということ。
シャルルは、圧力が一定の時、気体の体積は絶対温度に比例するという法則を発見しました。表にすると次のようになります(数値はあくまでわかりやすいようにした例です)。
| 体積 V | 10L | 20L | 30L | 40L |
| 温度 T | 10K | 20K | 30K | 40K |
V1 / T1 = V2 / T2(Vは体積、Tは絶対温度)


温度を高くすると熱運動が激しくなって体積は大きくなるんだね。
ボイルの法則とシャルルの法則を合わせたものです。気体の体積は圧力に反比例し、絶対温度に比例します。
P1V1 / T1 = P2V2 / T2

ボイル・シャルルの式を導き出してみましょう。
始めの状態の圧力をP1、体積をV1、温度をT1とします。次に温度を変化させないで圧力をP2に変化させます(途中の状態)。最後に圧力を一定に保ったまま温度をT2に変化させ、体積がV2に確定します。
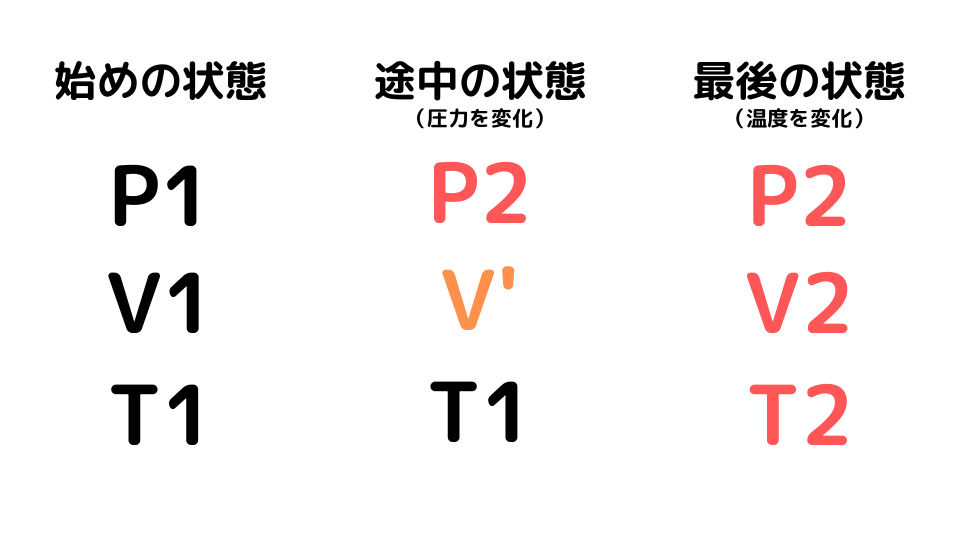
始めの状態→途中の状態
温度は変化しないのでボイルの法則が成り立ちます。
P1V1 = P2V’ …①
途中の状態→最後の状態
圧力は変化しないのでシャルルの法則が成り立ちます。
V’ / T1 = V2 / T2 …②
V’を除去する
①と②の式より、V’を除去します。②よりV’ = V2×T1 / T2を①に代入します。すると下の式を得ることができます。
P1V1 / T1 = P2V2 / T2

ボイル・シャルルの式が完成したね。